statistics — Mathematische Statistikfunktionen

Hinzugefügt in Version 3.4.

Quellcode: Lib/statistics.py

---

Dieses Modul stellt Funktionen zur Berechnung mathematischer Statistiken von numerischen Daten (Real-Werte) bereit.

Das Modul soll keine Konkurrenz zu Drittanbieterbibliotheken wie NumPy, SciPy oder proprietären, voll ausgestatteten Statistikpaketen für professionelle Statistiker wie Minitab, SAS und Matlab darstellen. Es ist für das Niveau von Grafik- und wissenschaftlichen Taschenrechnern ausgelegt.

Sofern nicht ausdrücklich anders angegeben, unterstützen diese Funktionen int, float, Decimal und Fraction. Das Verhalten bei anderen Typen (ob im numerischen Turm oder nicht) ist derzeit nicht unterstützt. Sammlungen mit einer Mischung von Typen sind ebenfalls undefiniert und implementierungsabhängig. Wenn Ihre Eingabedaten aus gemischten Typen bestehen, können Sie map() verwenden, um ein konsistentes Ergebnis zu erzielen, z. B.: map(float, input_data).

Einige Datensätze verwenden NaN (Not a Number)-Werte, um fehlende Daten darzustellen. Da NaNs eine ungewöhnliche Vergleichssemantik aufweisen, führen sie zu überraschenden oder undefinierten Verhaltensweisen in den Statistikfunktionen, die Daten sortieren oder Vorkommen zählen. Die betroffenen Funktionen sind median(), median_low(), median_high(), median_grouped(), mode(), multimode() und quantiles(). Die NaN-Werte sollten entfernt werden, bevor diese Funktionen aufgerufen werden.

>>> from statistics import median
>>> from math import isnan
>>> from itertools import filterfalse

>>> data = [20.7, float('NaN'),19.2, 18.3, float('NaN'), 14.4]
>>> sorted(data)  # This has surprising behavior
[20.7, nan, 14.4, 18.3, 19.2, nan]
>>> median(data)  # This result is unexpected
16.35

>>> sum(map(isnan, data))    # Number of missing values
2
>>> clean = list(filterfalse(isnan, data))  # Strip NaN values
>>> clean
[20.7, 19.2, 18.3, 14.4]
>>> sorted(clean)  # Sorting now works as expected
[14.4, 18.3, 19.2, 20.7]
>>> median(clean)       # This result is now well defined
18.75

Mittelwerte und Maße der zentralen Lage

Diese Funktionen berechnen einen Durchschnittswert oder einen typischen Wert aus einer Population oder einer Stichprobe.

mean()	Arithmetischer Mittelwert („Durchschnitt“) von Daten.
fmean()	Schneller arithmetischer Mittelwert mit Fließkommazahlen, mit optionaler Gewichtung.
geometric_mean()	Geometrischer Mittelwert von Daten.
harmonic_mean()	Harmonischer Mittelwert von Daten.
kde()	Schätzt die Wahrscheinlichkeitsdichtefunktion der Daten.
kde_random()	Zufällige Stichprobenziehung aus der von kde() erzeugten PDF.
median()	Median (mittlerer Wert) von Daten.
median_low()	Niedriger Median von Daten.
median_high()	Hoher Median von Daten.
median_grouped()	Median (50. Perzentil) von gruppierten Daten.
mode()	Einzelner Modus (häufigster Wert) von diskreten oder nominalen Daten.
multimode()	Liste von Modi (häufigste Werte) von diskreten oder nominalen Daten.
quantiles()	Teilt Daten in Intervalle mit gleicher Wahrscheinlichkeit auf.

Maße der Streuung

Diese Funktionen berechnen ein Maß dafür, wie stark die Population oder Stichprobe von den typischen oder durchschnittlichen Werten abweicht.

pstdev()	Standardabweichung der Population von Daten.
pvariance()	Varianz der Population von Daten.
stdev()	Stichproben-Standardabweichung von Daten.
variance()	Stichproben-Varianz von Daten.

Statistiken für Beziehungen zwischen zwei Eingaben

Diese Funktionen berechnen Statistiken für Beziehungen zwischen zwei Eingaben.

covariance()	Stichproben-Kovarianz für zwei Variablen.
correlation()	Pearson- und Spearman-Korrelationskoeffizienten.
linear_regression()	Steigung und Achsenabschnitt für einfache lineare Regression.

Funktionsdetails

Hinweis: Die Funktionen verlangen nicht, dass die ihnen übergebenen Daten sortiert sind. Aus Gründen der Lesbarkeit zeigen die meisten Beispiele jedoch sortierte Sequenzen an.

statistics.mean(data)

Gibt den arithmetischen Mittelwert der Stichprobe von data zurück, bei dem es sich um eine Sequenz oder einen Iterable handeln kann.

Der arithmetische Mittelwert ist die Summe der Daten, geteilt durch die Anzahl der Datenpunkte. Er wird üblicherweise als „Durchschnitt“ bezeichnet, obwohl er nur einer von vielen verschiedenen mathematischen Durchschnitten ist. Er ist ein Maß für die zentrale Lage der Daten.

Wenn data leer ist, wird StatisticsError ausgelöst.

Einige Anwendungsbeispiele

>>> mean([1, 2, 3, 4, 4])
2.8
>>> mean([-1.0, 2.5, 3.25, 5.75])
2.625

>>> from fractions import Fraction as F
>>> mean([F(3, 7), F(1, 21), F(5, 3), F(1, 3)])
Fraction(13, 21)

>>> from decimal import Decimal as D
>>> mean([D("0.5"), D("0.75"), D("0.625"), D("0.375")])
Decimal('0.5625')

Hinweis

Der Mittelwert wird stark von Ausreißern beeinflusst und ist nicht unbedingt ein typisches Beispiel für die Datenpunkte. Für ein robusteres, wenn auch weniger effizientes Maß für die zentrale Tendenz, siehe median().

Der Stichprobenmittelwert liefert eine unverzerrte Schätzung des wahren Populationsmittelwerts, sodass bei Durchschnittsbildung über alle möglichen Stichproben hinweg mean(sample) gegen den wahren Mittelwert der gesamten Population konvergiert. Wenn data die gesamte Population und nicht eine Stichprobe darstellt, ist mean(data) äquivalent zur Berechnung des wahren Populationsmittelwerts μ.

statistics.fmean(data, weights=None)

Konvertiert data in Floats und berechnet den arithmetischen Mittelwert.

Dies ist schneller als die Funktion mean() und gibt immer einen float zurück. data kann eine Sequenz oder ein Iterable sein. Wenn der Eingabedatensatz leer ist, wird ein StatisticsError ausgelöst.

>>> fmean([3.5, 4.0, 5.25])
4.25

Optionale Gewichtung wird unterstützt. Zum Beispiel weist ein Professor eine Note für einen Kurs zu, indem er Quizze mit 20 %, Hausaufgaben mit 20 %, eine Zwischenprüfung mit 30 % und eine Abschlussprüfung mit 30 % gewichtet.

>>> grades = [85, 92, 83, 91]
>>> weights = [0.20, 0.20, 0.30, 0.30]
>>> fmean(grades, weights)
87.6

Wenn weights angegeben wird, muss es die gleiche Länge wie data haben, andernfalls wird ein ValueError ausgelöst.

Hinzugefügt in Version 3.8.

Geändert in Version 3.11: Unterstützung für weights hinzugefügt.

statistics.geometric_mean(data)

Konvertiert data in Floats und berechnet den geometrischen Mittelwert.

Der geometrische Mittelwert gibt die zentrale Tendenz oder den typischen Wert der Daten unter Verwendung des Produkts der Werte (im Gegensatz zum arithmetischen Mittelwert, der deren Summe verwendet) an.

Löst eine StatisticsError aus, wenn der Eingabedatensatz leer ist, eine Null enthält oder einen negativen Wert enthält. data kann eine Sequenz oder ein Iterable sein.

Es werden keine besonderen Anstrengungen unternommen, um exakte Ergebnisse zu erzielen. (Dies kann sich jedoch in Zukunft ändern.)

>>> round(geometric_mean([54, 24, 36]), 1)
36.0

Hinzugefügt in Version 3.8.

statistics.harmonic_mean(data, weights=None)

Gibt den harmonischen Mittelwert von data, einer Sequenz oder einem Iterable von reellwertigen Zahlen, zurück. Wenn weights weggelassen wird oder None ist, wird von gleicher Gewichtung ausgegangen.

Der harmonische Mittelwert ist der Kehrwert des arithmetischen Mittelwerts der Kehrwerte der Daten. Beispielsweise ist der harmonische Mittelwert von drei Werten a, b und c äquivalent zu 3/(1/a + 1/b + 1/c). Wenn einer der Werte Null ist, ist das Ergebnis Null.

Der harmonische Mittelwert ist eine Art Durchschnitt, ein Maß für die zentrale Lage der Daten. Er ist oft geeignet, wenn Verhältnisse oder Raten gemittelt werden, z. B. Geschwindigkeiten.

Angenommen, ein Auto fährt 10 km mit 40 km/h, dann weitere 10 km mit 60 km/h. Wie hoch ist die Durchschnittsgeschwindigkeit?

>>> harmonic_mean([40, 60])
48.0

Angenommen, ein Auto fährt 40 km/h für 5 km und beschleunigt dann bei freier Fahrt auf 60 km/h für die restlichen 30 km der Strecke. Wie hoch ist die Durchschnittsgeschwindigkeit?

>>> harmonic_mean([40, 60], weights=[5, 30])
56.0

StatisticsError wird ausgelöst, wenn data leer ist, ein Element kleiner als Null ist oder die gewichtete Summe nicht positiv ist.

Der aktuelle Algorithmus bricht frühzeitig ab, wenn er auf eine Null in der Eingabe stößt. Das bedeutet, dass die nachfolgenden Eingaben nicht auf Gültigkeit geprüft werden. (Dieses Verhalten kann sich in Zukunft ändern.)

Hinzugefügt in Version 3.6.

Geändert in Version 3.10: Unterstützung für weights hinzugefügt.

statistics.kde(data, h, kernel='normal', *, cumulative=False)

Kernel Density Estimation (KDE): Erstellt eine kontinuierliche Wahrscheinlichkeitsdichtefunktion oder kumulative Verteilungsfunktion aus diskreten Stichproben.

Die Grundidee ist, die Daten mit einer Kernel-Funktion zu glätten, um Schlussfolgerungen über eine Population aus einer Stichprobe ziehen zu können.

Der Grad der Glättung wird durch den Skalierungsparameter h gesteuert, der als Bandbreite bezeichnet wird. Kleinere Werte betonen lokale Merkmale, während größere Werte glattere Ergebnisse liefern.

Der Kernel bestimmt die relativen Gewichte der Stichprobendatenpunkte. Im Allgemeinen spielt die Wahl der Kernel-Form nicht so eine große Rolle wie der einflussreichere Bandbreiten-Glättungsparameter.

Kernel, die jedem Stichprobendatenpunkt ein gewisses Gewicht geben, sind normal (gauss), logistic und sigmoid.

Kernel, die nur Stichprobendatenpunkten innerhalb der Bandbreite ein Gewicht geben, sind rechteckig (uniform), dreieckig, parabolisch (epanechnikov), quadratisch (biweight), triweight und kosinus.

Wenn cumulative wahr ist, wird eine kumulative Verteilungsfunktion zurückgegeben.

Eine StatisticsError wird ausgelöst, wenn die data-Sequenz leer ist.

Wikipedia hat ein Beispiel, in dem wir kde() verwenden können, um eine aus einer kleinen Stichprobe geschätzte Wahrscheinlichkeitsdichtefunktion zu erzeugen und zu plotten.

>>> sample = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> f_hat = kde(sample, h=1.5)
>>> xarr = [i/100 for i in range(-750, 1100)]
>>> yarr = [f_hat(x) for x in xarr]

Die Punkte in xarr und yarr können zur Erstellung eines PDF-Plots verwendet werden.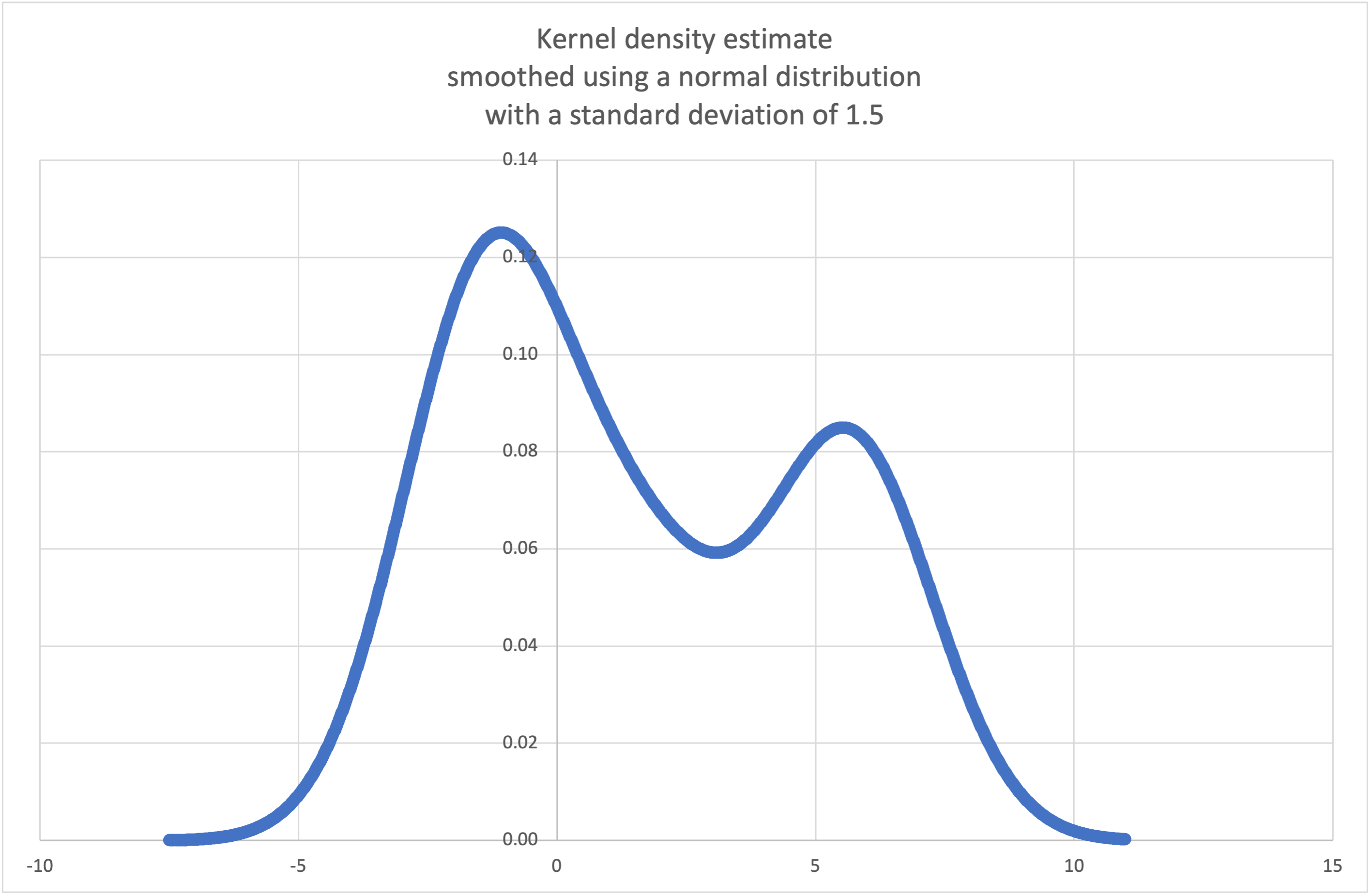

Hinzugefügt in Version 3.13.

statistics.kde_random(data, h, kernel='normal', *, seed=None)

Gibt eine Funktion zurück, die eine zufällige Auswahl aus der geschätzten Wahrscheinlichkeitsdichtefunktion generiert, die von kde(data, h, kernel) erzeugt wird.

Die Angabe eines seed ermöglicht reproduzierbare Auswahlen. In Zukunft können sich die Werte geringfügig ändern, wenn genauere Kernel-Inverse-CDF-Schätzungen implementiert werden. Der Seed kann eine Ganzzahl, eine Fließkommazahl, ein String oder Bytes sein.

Eine StatisticsError wird ausgelöst, wenn die data-Sequenz leer ist.

Im Anschluss an das Beispiel für kde() können wir kde_random() verwenden, um neue zufällige Auswahlen aus einer geschätzten Wahrscheinlichkeitsdichtefunktion zu generieren.

>>> data = [-2.1, -1.3, -0.4, 1.9, 5.1, 6.2]
>>> rand = kde_random(data, h=1.5, seed=8675309)
>>> new_selections = [rand() for i in range(10)]
>>> [round(x, 1) for x in new_selections]
[0.7, 6.2, 1.2, 6.9, 7.0, 1.8, 2.5, -0.5, -1.8, 5.6]

Hinzugefügt in Version 3.13.

statistics.median(data)

Gibt den Median (mittleren Wert) von numerischen Daten zurück, wobei die übliche Methode „Mittelwert der beiden mittleren Werte“ verwendet wird. Wenn data leer ist, wird StatisticsError ausgelöst. data kann eine Sequenz oder ein Iterable sein.

Der Median ist ein robustes Maß für die zentrale Lage und wird weniger von Ausreißern beeinflusst. Wenn die Anzahl der Datenpunkte ungerade ist, wird der mittlere Datenpunkt zurückgegeben.

>>> median([1, 3, 5])
3

Wenn die Anzahl der Datenpunkte gerade ist, wird der Median interpoliert, indem der Durchschnitt der beiden mittleren Werte gebildet wird.

>>> median([1, 3, 5, 7])
4.0

Dies ist geeignet, wenn Ihre Daten diskret sind und es Ihnen nichts ausmacht, dass der Median kein tatsächlicher Datenpunkt ist.

Wenn die Daten ordinal sind (unterstützen Ordnungsoperationen), aber nicht numerisch (unterstützen keine Addition), sollten Sie stattdessen median_low() oder median_high() verwenden.

statistics.median_low(data)

Gibt den niedrigen Median von numerischen Daten zurück. Wenn data leer ist, wird StatisticsError ausgelöst. data kann eine Sequenz oder ein Iterable sein.

Der niedrige Median ist immer ein Element des Datensatzes. Wenn die Anzahl der Datenpunkte ungerade ist, wird der mittlere Wert zurückgegeben. Wenn sie gerade ist, wird der kleinere der beiden mittleren Werte zurückgegeben.

>>> median_low([1, 3, 5])
3
>>> median_low([1, 3, 5, 7])
3

Verwenden Sie den niedrigen Median, wenn Ihre Daten diskret sind und Sie bevorzugen, dass der Median ein tatsächlicher Datenpunkt und keine Interpolation ist.

statistics.median_high(data)

Gibt den hohen Median von Daten zurück. Wenn data leer ist, wird StatisticsError ausgelöst. data kann eine Sequenz oder ein Iterable sein.

Der hohe Median ist immer ein Element des Datensatzes. Wenn die Anzahl der Datenpunkte ungerade ist, wird der mittlere Wert zurückgegeben. Wenn sie gerade ist, wird der größere der beiden mittleren Werte zurückgegeben.

>>> median_high([1, 3, 5])
3
>>> median_high([1, 3, 5, 7])
5

Verwenden Sie den hohen Median, wenn Ihre Daten diskret sind und Sie bevorzugen, dass der Median ein tatsächlicher Datenpunkt und keine Interpolation ist.

statistics.median_grouped(data, interval=1.0)

Schätzt den Median für numerische Daten, die um die Mittelpunkte aufeinanderfolgender Intervalle fester Breite gruppiert oder eingeteilt wurden.

Die data können beliebige Iterable mit numerischen Daten sein, wobei jeder Wert genau der Mittelpunkt eines Bins ist. Es muss mindestens ein Wert vorhanden sein.

Das interval ist die Breite jedes Bins.

Zum Beispiel könnten demografische Informationen in aufeinanderfolgende zehnjährige Altersgruppen zusammengefasst worden sein, wobei jede Gruppe durch die 5-Jahres-Mittelpunkte der Intervalle repräsentiert wird.

>>> from collections import Counter
>>> demographics = Counter({
...    25: 172,   # 20 to 30 years old
...    35: 484,   # 30 to 40 years old
...    45: 387,   # 40 to 50 years old
...    55:  22,   # 50 to 60 years old
...    65:   6,   # 60 to 70 years old
... })
...

Das 50. Perzentil (Median) ist die 536. Person von den 1071 Mitgliedern des Kohorten. Diese Person befindet sich in der Altersgruppe von 30 bis 40 Jahren.

Die reguläre Funktion median() würde annehmen, dass alle Personen in der Dreißiger-Altersgruppe genau 35 Jahre alt sind. Eine plausiblere Annahme ist, dass die 484 Mitglieder dieser Altersgruppe gleichmäßig zwischen 30 und 40 Jahre verteilt sind. Dafür verwenden wir median_grouped().

>>> data = list(demographics.elements())
>>> median(data)
35
>>> round(median_grouped(data, interval=10), 1)
37.5

Der Aufrufer ist dafür verantwortlich, sicherzustellen, dass die Datenpunkte durch exakte Vielfache des interval getrennt sind. Dies ist entscheidend für ein korrektes Ergebnis. Die Funktion überprüft diese Voraussetzung nicht.

Eingaben können jeder numerische Typ sein, der während des Interpolationsschritts in einen Float umgewandelt werden kann.

statistics.mode(data)

Gibt den einzelnen häufigsten Datenpunkt aus diskreten oder nominalen Daten zurück. Der Modus (sofern vorhanden) ist der typischste Wert und dient als Maß für die zentrale Lage.

Wenn es mehrere Modi mit derselben Häufigkeit gibt, wird der erste im data angetroffene Modus zurückgegeben. Wenn stattdessen der kleinste oder größte dieser Modi gewünscht wird, verwenden Sie min(multimode(data)) oder max(multimode(data)). Wenn die Eingabe data leer ist, wird StatisticsError ausgelöst.

mode geht von diskreten Daten aus und gibt einen einzelnen Wert zurück. Dies ist die Standardbehandlung des Modus, wie er üblicherweise in Schulen gelehrt wird.

>>> mode([1, 1, 2, 3, 3, 3, 3, 4])
3

Der Modus ist einzigartig, da er die einzige Statistik in diesem Paket ist, die auch für nominale (nicht-numerische) Daten gilt.

>>> mode(["red", "blue", "blue", "red", "green", "red", "red"])
'red'

Nur hashbare Eingaben werden unterstützt. Um den Typ set zu behandeln, sollten Sie eine Umwandlung in frozenset in Erwägung ziehen. Um den Typ list zu behandeln, sollten Sie eine Umwandlung in tuple in Erwägung ziehen. Für gemischte oder verschachtelte Eingaben sollten Sie diesen langsameren quadratischen Algorithmus in Erwägung ziehen, der nur auf Gleichheitstests beruht: max(data, key=data.count).

Geändert in Version 3.8: Behandelt jetzt multimodale Datensätze, indem der erste angetroffene Modus zurückgegeben wird. Zuvor wurde StatisticsError ausgelöst, wenn mehr als ein Modus gefunden wurde.

statistics.multimode(data)

Gibt eine Liste der am häufigsten vorkommenden Werte in der Reihenfolge zurück, in der sie zuerst in data angetroffen wurden. Gibt mehr als ein Ergebnis zurück, wenn es mehrere Modi gibt, oder eine leere Liste, wenn data leer ist.

>>> multimode('aabbbbccddddeeffffgg')
['b', 'd', 'f']
>>> multimode('')
[]

Hinzugefügt in Version 3.8.

statistics.pstdev(data, mu=None)

Gibt die Standardabweichung der Population zurück (die Quadratwurzel der Populationsvarianz). Siehe pvariance() für Argumente und weitere Details.

>>> pstdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
0.986893273527251

statistics.pvariance(data, mu=None)

Gibt die Varianz der Population von data zurück, einer nicht-leeren Sequenz oder einem Iterable von reellwertigen Zahlen. Varianz, oder zweites Moment um den Mittelwert, ist ein Maß für die Variabilität (Streuung oder Dispersion) von Daten. Eine große Varianz deutet darauf hin, dass die Daten weit gestreut sind; eine kleine Varianz deutet darauf hin, dass sie eng um den Mittelwert gruppiert sind.

Wenn das optionale zweite Argument mu gegeben ist, sollte es der Populationsmittelwert der Daten sein. Es kann auch verwendet werden, um das zweite Moment um einen Punkt zu berechnen, der nicht der Mittelwert ist. Wenn es fehlt oder None (Standard) ist, wird der arithmetische Mittelwert automatisch berechnet.

Verwenden Sie diese Funktion, um die Varianz aus der gesamten Population zu berechnen. Zur Schätzung der Varianz aus einer Stichprobe ist die Funktion variance() normalerweise die bessere Wahl.

Löst StatisticsError aus, wenn data leer ist.

Beispiele

>>> data = [0.0, 0.25, 0.25, 1.25, 1.5, 1.75, 2.75, 3.25]
>>> pvariance(data)
1.25

Wenn Sie bereits den Mittelwert Ihrer Daten berechnet haben, können Sie ihn als optionales zweites Argument mu übergeben, um eine Neuberechnung zu vermeiden.

>>> mu = mean(data)
>>> pvariance(data, mu)
1.25

Dezimale und Brüche werden unterstützt.

>>> from decimal import Decimal as D
>>> pvariance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('24.815')

>>> from fractions import Fraction as F
>>> pvariance([F(1, 4), F(5, 4), F(1, 2)])
Fraction(13, 72)

Hinweis

Wenn mit der gesamten Population aufgerufen, ergibt dies die Populationsvarianz σ². Wenn stattdessen mit einer Stichprobe aufgerufen, ist dies die verzerrte Stichprobenvarianz s², auch bekannt als Varianz mit N Freiheitsgraden.

Wenn Sie irgendwie den wahren Populationsmittelwert μ kennen, können Sie diese Funktion verwenden, um die Varianz einer Stichprobe zu berechnen, und den bekannten Populationsmittelwert als zweites Argument übergeben. Vorausgesetzt, die Datenpunkte sind eine Zufallsstichprobe der Population, ist das Ergebnis eine unverzerrte Schätzung der Populationsvarianz.

statistics.stdev(data, xbar=None)

Gibt die Stichproben-Standardabweichung zurück (die Quadratwurzel der Stichprobenvarianz). Siehe variance() für Argumente und weitere Details.

>>> stdev([1.5, 2.5, 2.5, 2.75, 3.25, 4.75])
1.0810874155219827

statistics.variance(data, xbar=None)

Gibt die Stichprobenvarianz von data zurück, einem Iterable von mindestens zwei reellwertigen Zahlen. Varianz, oder zweites Moment um den Mittelwert, ist ein Maß für die Variabilität (Streuung oder Dispersion) von Daten. Eine große Varianz deutet darauf hin, dass die Daten weit gestreut sind; eine kleine Varianz deutet darauf hin, dass sie eng um den Mittelwert gruppiert sind.

Wenn das optionale zweite Argument xbar gegeben ist, sollte es der Stichprobenmittelwert von data sein. Wenn es fehlt oder None (Standard) ist, wird der Mittelwert automatisch berechnet.

Verwenden Sie diese Funktion, wenn Ihre Daten eine Stichprobe aus einer Population sind. Zur Berechnung der Varianz aus der gesamten Population siehe pvariance().

Löst StatisticsError aus, wenn data weniger als zwei Werte hat.

Beispiele

>>> data = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]
>>> variance(data)
1.3720238095238095

Wenn Sie bereits den Stichprobenmittelwert Ihrer Daten berechnet haben, können Sie ihn als optionales zweites Argument xbar übergeben, um eine Neuberechnung zu vermeiden.

>>> m = mean(data)
>>> variance(data, m)
1.3720238095238095

Diese Funktion versucht nicht zu überprüfen, ob Sie den tatsächlichen Mittelwert als xbar übergeben haben. Die Verwendung beliebiger Werte für xbar kann zu ungültigen oder unmöglichen Ergebnissen führen.

Dezimal- und Bruchausdrücke werden unterstützt.

>>> from decimal import Decimal as D
>>> variance([D("27.5"), D("30.25"), D("30.25"), D("34.5"), D("41.75")])
Decimal('31.01875')

>>> from fractions import Fraction as F
>>> variance([F(1, 6), F(1, 2), F(5, 3)])
Fraction(67, 108)

Hinweis

Dies ist die Stichprobenvarianz s² mit Bessels Korrektur, auch bekannt als Varianz mit N-1 Freiheitsgraden. Vorausgesetzt, die Datenpunkte sind repräsentativ (z. B. unabhängig und identisch verteilt), sollte das Ergebnis eine unverzerrte Schätzung der wahren Populationsvarianz sein.

Wenn Sie irgendwie den tatsächlichen Populationsmittelwert μ kennen, sollten Sie ihn der Funktion pvariance() als Parameter mu übergeben, um die Varianz einer Stichprobe zu erhalten.

statistics.quantiles(data, *, n=4, method='exclusive')

Teilt data in n kontinuierliche Intervalle mit gleicher Wahrscheinlichkeit auf. Gibt eine Liste von n - 1 Schnittpunkten zurück, die die Intervalle trennen.

Setzen Sie n auf 4 für Quartile (Standard). Setzen Sie n auf 10 für Dezile. Setzen Sie n auf 100 für Perzentile, was die 99 Schnittpunkte ergibt, die data in 100 gleich große Gruppen aufteilen. Löst StatisticsError aus, wenn n nicht mindestens 1 ist.

Die data können beliebige Iterable mit Stichprobendaten enthalten. Für aussagekräftige Ergebnisse sollte die Anzahl der Datenpunkte in data größer als n sein. Löst StatisticsError aus, wenn nicht mindestens ein Datenpunkt vorhanden ist.

Die Schnittpunkte werden linear aus den beiden nächsten Datenpunkten interpoliert. Wenn beispielsweise ein Schnittpunkt ein Drittel der Entfernung zwischen zwei Stichprobenwerten, 100 und 112, liegt, wird der Schnittpunkt zu 104 ausgewertet.

Die methode zur Berechnung von Quantilen kann variieren, je nachdem, ob die Daten die niedrigsten und höchsten möglichen Werte aus der Population einschließen oder ausschließen.

Die Standard-methode ist „exclusive“ und wird für Daten verwendet, die aus einer Population entnommen wurden, die extremere Werte als die in den Stichproben gefundenen haben kann. Der Anteil der Population, der unter dem i-ten von m sortierten Datenpunkten liegt, wird als i / (m + 1) berechnet. Bei neun Stichprobenwerten werden diese sortiert und die folgenden Perzentile zugewiesen: 10 %, 20 %, 30 %, 40 %, 50 %, 60 %, 70 %, 80 %, 90 %.

Das Setzen der methode auf „inclusive“ wird zur Beschreibung von Populationsdaten oder für Stichproben verwendet, die bekanntermaßen die extremsten Werte aus der Population enthalten. Der Mindestwert in data wird als 0. Perzentil und der Höchstwert als 100. Perzentil behandelt. Der Anteil der Population, der unter dem i-ten von m sortierten Datenpunkten liegt, wird als (i - 1) / (m - 1) berechnet. Bei elf Stichprobenwerten werden diese sortiert und die folgenden Perzentile zugewiesen: 0 %, 10 %, 20 %, 30 %, 40 %, 50 %, 60 %, 70 %, 80 %, 90 %, 100 %.

# Decile cut points for empirically sampled data
>>> data = [105, 129, 87, 86, 111, 111, 89, 81, 108, 92, 110,
...         100, 75, 105, 103, 109, 76, 119, 99, 91, 103, 129,
...         106, 101, 84, 111, 74, 87, 86, 103, 103, 106, 86,
...         111, 75, 87, 102, 121, 111, 88, 89, 101, 106, 95,
...         103, 107, 101, 81, 109, 104]
>>> [round(q, 1) for q in quantiles(data, n=10)]
[81.0, 86.2, 89.0, 99.4, 102.5, 103.6, 106.0, 109.8, 111.0]

Hinzugefügt in Version 3.8.

Geändert in Version 3.13: Löst keine Ausnahme mehr für eine Eingabe mit nur einem einzigen Datenpunkt aus. Dies ermöglicht die schrittweise Erstellung von Quantilschätzungen mit jedem neuen Datenpunkt, die mit jedem neuen Datenpunkt allmählich verfeinert werden.

statistics.covariance(x, y, /)

Gibt die Stichprobenkovarianz von zwei Eingaben x und y zurück. Kovarianz ist ein Maß für die gemeinsame Variabilität zweier Eingaben.

Beide Eingaben müssen die gleiche Länge haben (nicht weniger als zwei), andernfalls wird ein StatisticsError ausgelöst.

Beispiele

>>> x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> y = [1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> covariance(x, y)
0.75
>>> z = [9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> covariance(x, z)
-7.5
>>> covariance(z, x)
-7.5

Hinzugefügt in Version 3.10.

statistics.correlation(x, y, /, *, method='linear')

Gibt den Pearson-Korrelationskoeffizienten für zwei Eingaben zurück. Der Pearson-Korrelationskoeffizient r nimmt Werte zwischen -1 und +1 an. Er misst die Stärke und Richtung einer linearen Beziehung.

Wenn method "ranked" ist, wird der Rangkorrelationskoeffizient nach Spearman für zwei Eingaben berechnet. Die Daten werden durch Ränge ersetzt. Gleichstände werden gemittelt, sodass gleiche Werte denselben Rang erhalten. Der resultierende Koeffizient misst die Stärke einer monotonen Beziehung.

Der Rangkorrelationskoeffizient nach Spearman eignet sich für ordinale Daten oder für kontinuierliche Daten, die die Anforderung der linearen Proportionalität für den Pearson-Korrelationskoeffizienten nicht erfüllen.

Beide Eingaben müssen die gleiche Länge haben (nicht weniger als zwei) und müssen nicht konstant sein, andernfalls wird ein StatisticsError ausgelöst.

Beispiel mit Keplerschen Gesetzen der Planetenbewegung

>>> # Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and  Neptune
>>> orbital_period = [88, 225, 365, 687, 4331, 10_756, 30_687, 60_190]    # days
>>> dist_from_sun = [58, 108, 150, 228, 778, 1_400, 2_900, 4_500] # million km

>>> # Show that a perfect monotonic relationship exists
>>> correlation(orbital_period, dist_from_sun, method='ranked')
1.0

>>> # Observe that a linear relationship is imperfect
>>> round(correlation(orbital_period, dist_from_sun), 4)
0.9882

>>> # Demonstrate Kepler's third law: There is a linear correlation
>>> # between the square of the orbital period and the cube of the
>>> # distance from the sun.
>>> period_squared = [p * p for p in orbital_period]
>>> dist_cubed = [d * d * d for d in dist_from_sun]
>>> round(correlation(period_squared, dist_cubed), 4)
1.0

Hinzugefügt in Version 3.10.

Geändert in Version 3.12: Unterstützung für den Rangkorrelationskoeffizienten nach Spearman hinzugefügt.

statistics.linear_regression(x, y, /, *, proportional=False)

Gibt die Steigung und den Achsenabschnitt der Parameter einer einfachen linearen Regression zurück, die mit der Methode der kleinsten Quadrate geschätzt wurden. Die einfache lineare Regression beschreibt die Beziehung zwischen einer unabhängigen Variable x und einer abhängigen Variable y in Form dieser linearen Funktion

y = Steigung * x + Achsenabschnitt + Rauschen

wobei Steigung und Achsenabschnitt die geschätzten Regressionsparameter sind und Rauschen die Variabilität der Daten darstellt, die nicht durch die lineare Regression erklärt wurde (sie ist gleich der Differenz zwischen vorhergesagten und tatsächlichen Werten der abhängigen Variable).

Beide Eingaben müssen die gleiche Länge haben (nicht weniger als zwei), und die unabhängige Variable x darf nicht konstant sein; andernfalls wird ein StatisticsError ausgelöst.

Zum Beispiel können wir die Veröffentlichungstermine der Monty Python-Filme verwenden, um die kumulative Anzahl der von Monty Python produzierten Filme bis 2019 vorherzusagen, unter der Annahme, dass sie das Tempo beibehalten hätten.

>>> year = [1971, 1975, 1979, 1982, 1983]
>>> films_total = [1, 2, 3, 4, 5]
>>> slope, intercept = linear_regression(year, films_total)
>>> round(slope * 2019 + intercept)
16

Wenn proportional wahr ist, wird angenommen, dass die unabhängige Variable x und die abhängige Variable y direkt proportional sind. Die Daten werden an eine Linie angepasst, die durch den Ursprung verläuft. Da der Achsenabschnitt immer 0,0 sein wird, vereinfacht sich die zugrunde liegende lineare Funktion zu

y = Steigung * x + Rauschen

Fortsetzung des Beispiels aus correlation() sehen wir, wie gut ein Modell, das auf Hauptplaneten basiert, die Umlaufbahnen von Zwergplaneten vorhersagen kann

>>> model = linear_regression(period_squared, dist_cubed, proportional=True)
>>> slope = model.slope

>>> # Dwarf planets:   Pluto,  Eris,    Makemake, Haumea, Ceres
>>> orbital_periods = [90_560, 204_199, 111_845, 103_410, 1_680]  # days
>>> predicted_dist = [math.cbrt(slope * (p * p)) for p in orbital_periods]
>>> list(map(round, predicted_dist))
[5912, 10166, 6806, 6459, 414]

>>> [5_906, 10_152, 6_796, 6_450, 414]  # actual distance in million km
[5906, 10152, 6796, 6450, 414]

Hinzugefügt in Version 3.10.

Geändert in Version 3.11: Unterstützung für proportional hinzugefügt.

Ausnahmen

Eine einzelne Ausnahme wird definiert

exception statistics.StatisticsError

Unterklasse von ValueError für statistisch relevante Ausnahmen.

NormalDist Objekte

NormalDist ist ein Werkzeug zur Erstellung und Manipulation von Normalverteilungen einer Zufallsvariable. Es ist eine Klasse, die den Mittelwert und die Standardabweichung von Messdaten als eine einzige Einheit behandelt.

Normalverteilungen ergeben sich aus dem Zentralen Grenzwertsatz und haben eine breite Palette von Anwendungen in der Statistik.

class statistics.NormalDist(mu=0.0, sigma=1.0)

Gibt ein neues NormalDist-Objekt zurück, bei dem mu den arithmetischen Mittelwert und sigma die Standardabweichung darstellt.

Wenn sigma negativ ist, wird ein StatisticsError ausgelöst.

mean

Eine schreibgeschützte Eigenschaft für den arithmetischen Mittelwert einer Normalverteilung.

median

Eine schreibgeschützte Eigenschaft für den Median einer Normalverteilung.

mode

Eine schreibgeschützte Eigenschaft für den Modalwert einer Normalverteilung.

stdev

Eine schreibgeschützte Eigenschaft für die Standardabweichung einer Normalverteilung.

variance

Eine schreibgeschützte Eigenschaft für die Varianz einer Normalverteilung. Gleich dem Quadrat der Standardabweichung.

classmethod from_samples(data)

Erstellt eine Normalverteilung mit den Parametern mu und sigma, die aus den data mit fmean() und stdev() geschätzt wurden.

Die data können ein beliebiger Iterable sein und sollten Werte enthalten, die in den Typ float konvertiert werden können. Wenn data weniger als zwei Elemente enthält, wird ein StatisticsError ausgelöst, da mindestens ein Punkt zur Schätzung eines zentralen Wertes und mindestens zwei Punkte zur Schätzung der Streuung erforderlich sind.

samples(n, *, seed=None)

Generiert n zufällige Stichproben für einen gegebenen Mittelwert und eine gegebene Standardabweichung. Gibt eine Liste von float-Werten zurück.

Wenn seed angegeben ist, wird eine neue Instanz des zugrunde liegenden Zufallszahlengenerators erstellt. Dies ist nützlich, um reproduzierbare Ergebnisse zu erzielen, auch in einer Multi-Threading-Umgebung.

Geändert in Version 3.13.

Umstellung auf einen schnelleren Algorithmus. Um Stichproben aus früheren Versionen zu reproduzieren, verwenden Sie random.seed() und random.gauss().

pdf(x)

Mithilfe einer Wahrscheinlichkeitsdichtefunktion (pdf) wird die relative Wahrscheinlichkeit berechnet, dass eine Zufallsvariable X nahe dem gegebenen Wert x liegt. Mathematisch ist dies der Grenzwert des Verhältnisses P(x <= X < x+dx) / dx, wenn dx gegen Null geht.

Die relative Wahrscheinlichkeit wird als Wahrscheinlichkeit eines Stichprobenereignisses in einem engen Bereich dividiert durch die Breite des Bereichs berechnet (daher das Wort "Dichte"). Da die Wahrscheinlichkeit relativ zu anderen Punkten ist, kann ihr Wert größer als 1.0 sein.

cdf(x)

Mithilfe einer kumulativen Verteilungsfunktion (cdf) wird die Wahrscheinlichkeit berechnet, dass eine Zufallsvariable X kleiner oder gleich x ist. Mathematisch wird dies geschrieben als P(X <= x).

inv_cdf(p)

Berechnet die inverse kumulative Verteilungsfunktion, auch bekannt als Quantilfunktion oder Prozentpunktfunktion. Mathematisch wird sie geschrieben als x : P(X <= x) = p.

Findet den Wert x der Zufallsvariable X, so dass die Wahrscheinlichkeit, dass die Variable kleiner oder gleich diesem Wert ist, der gegebenen Wahrscheinlichkeit p entspricht.

overlap(other)

Misst die Übereinstimmung zwischen zwei Normalwahrscheinlichkeitsverteilungen. Gibt einen Wert zwischen 0,0 und 1,0 zurück, der die überlappende Fläche der beiden Wahrscheinlichkeitsdichtefunktionen darstellt.

quantiles(n=4)

Teilt die Normalverteilung in n kontinuierliche Intervalle mit gleicher Wahrscheinlichkeit. Gibt eine Liste von (n - 1) Schnittpunkten zurück, die die Intervalle trennen.

Setzen Sie n auf 4 für Quartile (Standard). Setzen Sie n auf 10 für Dezile. Setzen Sie n auf 100 für Perzentile, was die 99 Schnittpunkte ergibt, die die Normalverteilung in 100 gleich große Gruppen unterteilen.

zscore(x)

Berechnet den Standardwert (Z-Score), der x in Bezug auf die Anzahl der Standardabweichungen oberhalb oder unterhalb des Mittelwerts der Normalverteilung beschreibt: (x - Mittelwert) / StdAbw).

Hinzugefügt in Version 3.9.

Instanzen von NormalDist unterstützen Addition, Subtraktion, Multiplikation und Division durch eine Konstante. Diese Operationen werden für Translation und Skalierung verwendet. Zum Beispiel

>>> temperature_february = NormalDist(5, 2.5)             # Celsius
>>> temperature_february * (9/5) + 32                     # Fahrenheit
NormalDist(mu=41.0, sigma=4.5)

Die Division einer Konstante durch eine Instanz von NormalDist wird nicht unterstützt, da das Ergebnis keine Normalverteilung wäre.

Da Normalverteilungen aus additiven Effekten unabhängiger Variablen entstehen, ist es möglich, zwei unabhängige, normalverteilte Zufallsvariablen zu addieren und zu subtrahieren, die als Instanzen von NormalDist dargestellt werden. Zum Beispiel

>>> birth_weights = NormalDist.from_samples([2.5, 3.1, 2.1, 2.4, 2.7, 3.5])
>>> drug_effects = NormalDist(0.4, 0.15)
>>> combined = birth_weights + drug_effects
>>> round(combined.mean, 1)
3.1
>>> round(combined.stdev, 1)
0.5

Hinzugefügt in Version 3.8.

Beispiele und Rezepte

Klassische Wahrscheinlichkeitsprobleme

NormalDist löst ohne Weiteres klassische Wahrscheinlichkeitsprobleme.

Beispielsweise, gegeben historische Daten für SAT-Prüfungen, die zeigen, dass die Punktzahlen normalverteilt sind mit einem Mittelwert von 1060 und einer Standardabweichung von 195, bestimmen Sie den Prozentsatz der Schüler mit Testergebnissen zwischen 1100 und 1200, gerundet auf die nächste ganze Zahl

>>> sat = NormalDist(1060, 195)
>>> fraction = sat.cdf(1200 + 0.5) - sat.cdf(1100 - 0.5)
>>> round(fraction * 100.0, 1)
18.4

Finden Sie die Quartile und Dezile für die SAT-Punktzahlen

>>> list(map(round, sat.quantiles()))
[928, 1060, 1192]
>>> list(map(round, sat.quantiles(n=10)))
[810, 896, 958, 1011, 1060, 1109, 1162, 1224, 1310]

Monte-Carlo-Inputs für Simulationen

Um die Verteilung für ein Modell zu schätzen, das analytisch nicht leicht zu lösen ist, kann NormalDist Eingabestichproben für eine Monte-Carlo-Simulation generieren

>>> def model(x, y, z):
...     return (3*x + 7*x*y - 5*y) / (11 * z)
...
>>> n = 100_000
>>> X = NormalDist(10, 2.5).samples(n, seed=3652260728)
>>> Y = NormalDist(15, 1.75).samples(n, seed=4582495471)
>>> Z = NormalDist(50, 1.25).samples(n, seed=6582483453)
>>> quantiles(map(model, X, Y, Z))
[1.4591308524824727, 1.8035946855390597, 2.175091447274739]

Approximation von Binomialverteilungen

Normalverteilungen können verwendet werden, um Binomialverteilungen zu approximieren, wenn die Stichprobengröße groß ist und die Erfolgswahrscheinlichkeit nahe 50 % liegt.

Zum Beispiel hat eine Open-Source-Konferenz 750 Teilnehmer und zwei Räume mit einer Kapazität von 500 Personen. Es gibt einen Vortrag über Python und einen über Ruby. Auf früheren Konferenzen bevorzugten 65 % der Teilnehmer, Python-Vorträge zu hören. Unter der Annahme, dass sich die Präferenzen der Bevölkerung nicht geändert haben, wie hoch ist die Wahrscheinlichkeit, dass der Python-Raum seine Kapazitätsgrenzen einhält?

>>> n = 750             # Sample size
>>> p = 0.65            # Preference for Python
>>> q = 1.0 - p         # Preference for Ruby
>>> k = 500             # Room capacity

>>> # Approximation using the cumulative normal distribution
>>> from math import sqrt
>>> round(NormalDist(mu=n*p, sigma=sqrt(n*p*q)).cdf(k + 0.5), 4)
0.8402

>>> # Exact solution using the cumulative binomial distribution
>>> from math import comb, fsum
>>> round(fsum(comb(n, r) * p**r * q**(n-r) for r in range(k+1)), 4)
0.8402

>>> # Approximation using a simulation
>>> from random import seed, binomialvariate
>>> seed(8675309)
>>> mean(binomialvariate(n, p) <= k for i in range(10_000))
0.8406

Naive Bayes'scher Klassifikator

Normalverteilungen treten häufig bei maschinellen Lernproblemen auf.

Wikipedia hat ein gutes Beispiel für einen Naive Bayes-Klassifikator. Die Herausforderung besteht darin, das Geschlecht einer Person anhand von Messungen von normalverteilten Merkmalen wie Größe, Gewicht und Fußgröße vorherzusagen.

Wir erhalten einen Trainingsdatensatz mit Messungen von acht Personen. Die Messungen werden als normalverteilt angenommen, daher fassen wir die Daten mit NormalDist zusammen

>>> height_male = NormalDist.from_samples([6, 5.92, 5.58, 5.92])
>>> height_female = NormalDist.from_samples([5, 5.5, 5.42, 5.75])
>>> weight_male = NormalDist.from_samples([180, 190, 170, 165])
>>> weight_female = NormalDist.from_samples([100, 150, 130, 150])
>>> foot_size_male = NormalDist.from_samples([12, 11, 12, 10])
>>> foot_size_female = NormalDist.from_samples([6, 8, 7, 9])

Als Nächstes stoßen wir auf eine neue Person, deren Merkmalsmessungen bekannt sind, deren Geschlecht aber unbekannt ist

>>> ht = 6.0        # height
>>> wt = 130        # weight
>>> fs = 8          # foot size

Beginnend mit einer 50 %igen A-priori-Wahrscheinlichkeit für männlich oder weiblich berechnen wir die A-posteriori-Wahrscheinlichkeit als das A-priori mal das Produkt der Likelihoods für die Merkmalsmessungen gegeben das Geschlecht

>>> prior_male = 0.5
>>> prior_female = 0.5
>>> posterior_male = (prior_male * height_male.pdf(ht) *
...                   weight_male.pdf(wt) * foot_size_male.pdf(fs))

>>> posterior_female = (prior_female * height_female.pdf(ht) *
...                     weight_female.pdf(wt) * foot_size_female.pdf(fs))

Die endgültige Vorhersage gilt der größten A-posteriori-Wahrscheinlichkeit. Dies ist bekannt als Maximum a Posteriori oder MAP

>>> 'male' if posterior_male > posterior_female else 'female'
'female'